
神经网络权重初始化问题的思考
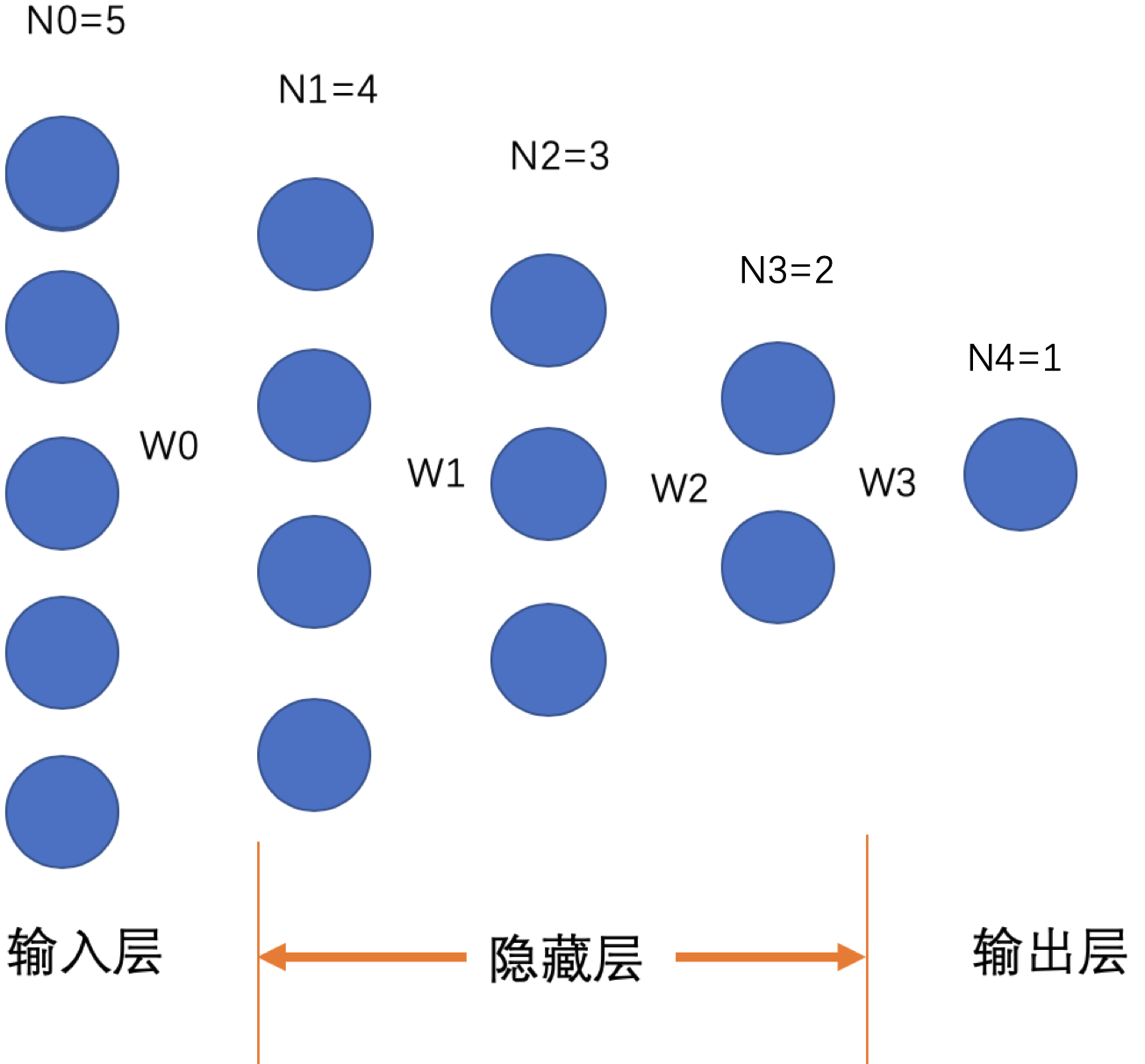
问题概述 众所周知,神经网络权重不能初始化为常数,更不能全部初始化为0。依据反向传播的思想可知:每个权重的更新梯度与其之后相关的权重、神经元的输入、输出和其前一个神经元的输出有关(这里不进行具体推导)。网上很多相关文章说不能初始化为0或者常数,这个结论肯定是正确的。但是原因却不是这样会导致权重不更新了。其实完全错误,只要有误差,就会更新。 神经网络模型定义 现假设神经网络的通用形式如下: 有一个输入层,n个隐藏层,一个输出层。其中输入层和第1个隐藏层的参数权重为,第1个和第2个隐藏层之权重为,以此类推:第n个隐藏层和输出层之间参数权重为。其中输入层神经元个数为,第个隐藏层的神经元个数为,输出层的神经元个数,则。如有一个"输入层+3层隐藏层+输出层"构成的网络,且输入层、输出层神经元个数为5、1,隐藏层的神经..
Read more

SGD、Momentum、RMSProp、Adam等优化算法比较
公式化及解释 简单理了下深度学习中常用的集中参数优化方法,用相对统一的形式规整了下: 算法名称 公式 解释 牛顿法 为第t-1轮迭代时海森矩阵逆矩阵,即目标函数对参数二阶导数。 梯度下降(GD) 使用所有数据进行梯度下降 随机梯度下降(SGD) 使用单个数据进行梯度下降 批量梯度下降(Mini-batch GD) 使用每一小批数据进行梯度下降 (即GD与SGD的折中) Momentum 利用累计的指数加权梯度-动量即惯性,作为每次权重更新的梯度 Nesterov Momentum 在Momentum的基础上根据下一步的新权重计算新梯度("往前多看一步") AdaGrad 不同参数有各自的自适应学习率,即全局学习率除以累计梯度平方和 RMS..
Read more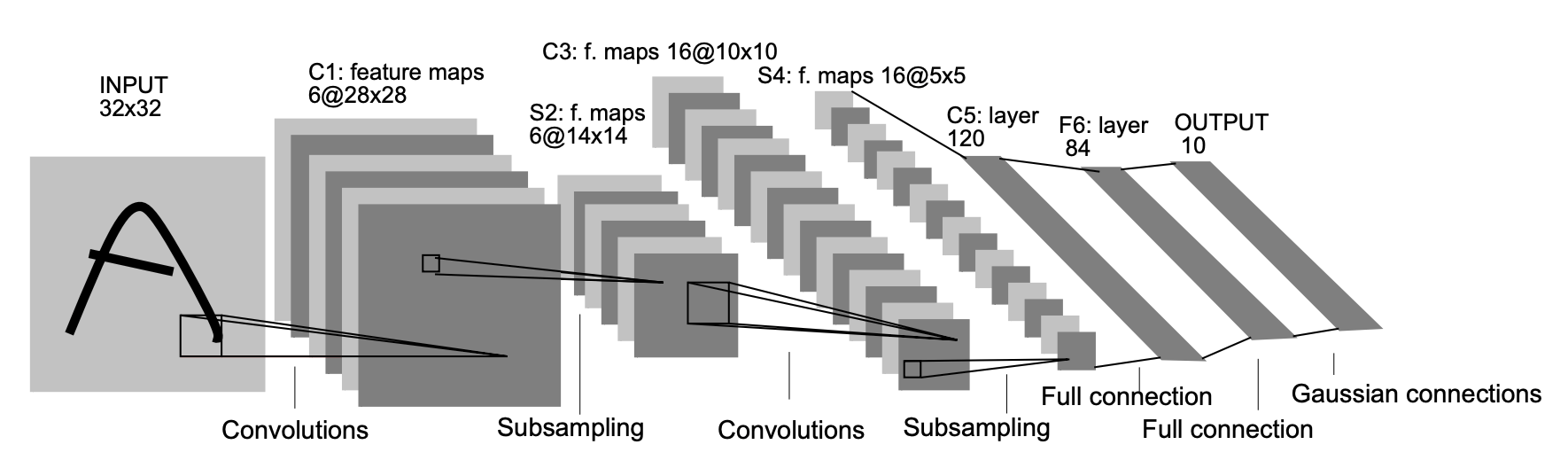

深度神经网络架构
LeNet LeNet是最早发布的卷积神经网络之一,因其在计算机视觉任务中的高效性能而受到广泛关注。 这个模型是由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的(并以其命名),目的是识别图像中的手写数字。 利用卷积、池化、激活函数、全连接层等操作提取特征(这也奠定了后续所有卷积神经网络的基本特性) 卷积操作实现参数共享,相比较全连接操作大大降低了参数量 LeNet又名LeNet5,是因为在LeNet网络中使用的均是 5×5 的卷积核,如下图所示: 图片来自原paper AlexNet AlexNet在2012年ImageNet挑战赛中取得了轰动一时的成绩,它首次证明了学习到的特征可以超越SIFT、HOG、Bags of Visual Words等手工设计的特征,同时也首..
Read more