概述
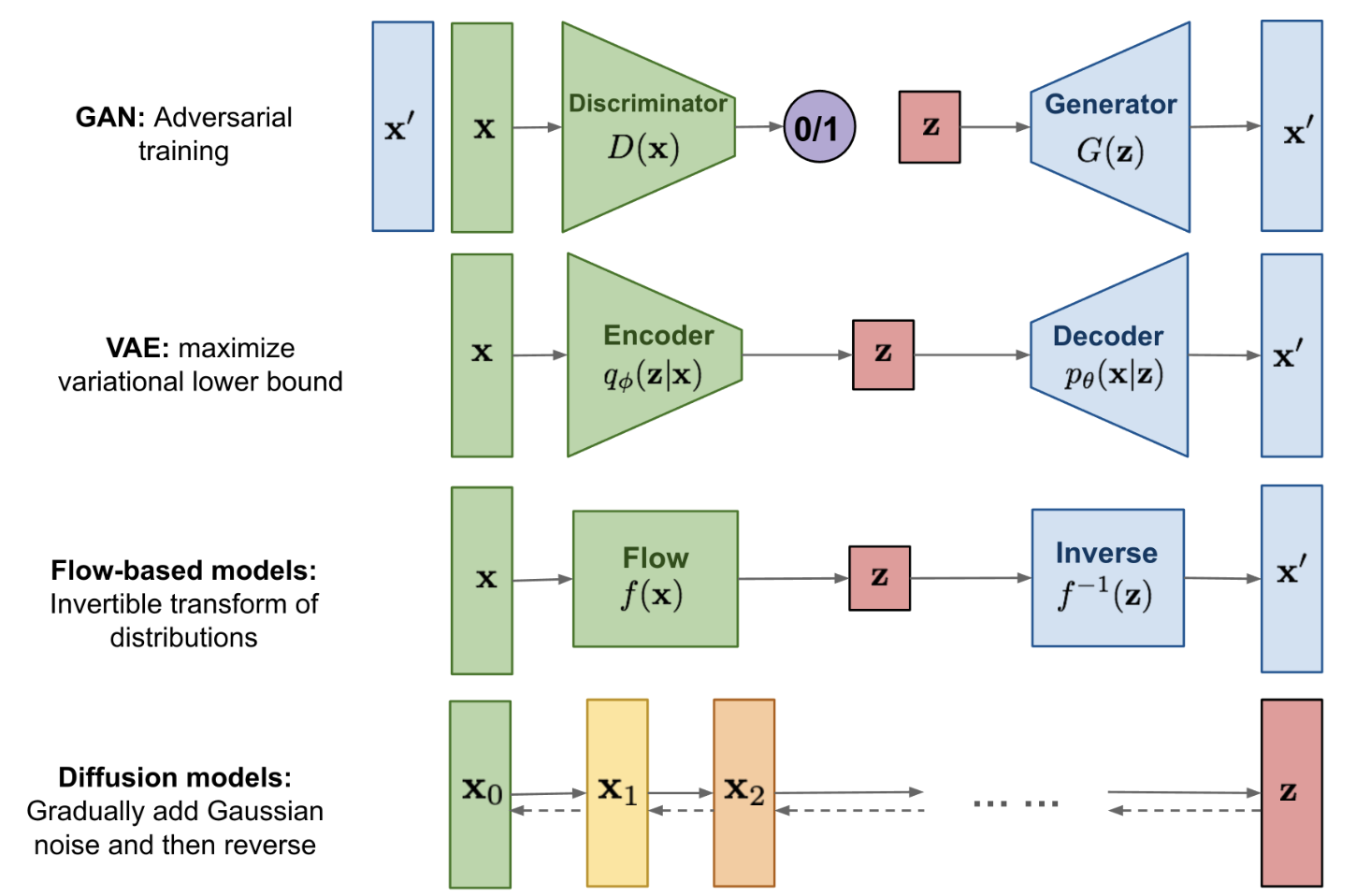
Diffusion属于生成模型的一种，相比较于GAN等其他生成模型，Diffusion模型最大的不同之处就在于其latent code是和原输入图相同尺寸的。Diffusion模型其实也可以看成是一个隐变量模型，并且与VAE,GAN的单隐变量不同，其可以看成存在多个隐变量(即加噪过程中的每个加噪结果都可以看成一个隐变量)。Diffusion模型总体包括前向加噪和逆向去噪两个过程:
- 前向过程-加噪扩散:对给定的真实图像
不断添加高斯噪声，经过中间状态 最终变成纯高斯噪声 - 逆向过程-去噪生成:从完全的纯噪声
不断去噪，经过中间状态 最终变成其对应的真实图像
上面两个过程示意图可以表示如下:
图中的
前向过程-加噪扩散
前向过程就是对给定的真实图像
前向单步:前向过程中间的某一步(
)可表示为条件概率: 而且其实可以直观看到整个前向的过程是一个马尔科夫的过程：即当前的时刻的结果( )只与其前一个结果( )有关而与起始状态( )无关，换句话说就是:在仅仅知道前一个状态 的条件下就可以得到 了，无需其他条件。所以根据马尔科夫链的性质我们也可以得到: 这个小细节后面会用到。此外这种预先定义好的方差设计规则我们也叫做Variance shedule，比如DDPM中就采用一个线性变换Variance shedule: betas = torch.linspace(start=0.0001, end=0.02, steps=1000)而至于这里方差
为什么设置在0~1之间，均值系数又为什么设置成 ，后面会进一步讨论。 总体前向:整个前向过程(
)可以表达为条件概率下的联合概率:
现在我们思考一下:
上述的重参数化不仅使得模型可微，还使得前向过程对
其中
逆向过程-去噪生成
逆向过程就是从完全的纯噪声
回顾一下，前向过程中我们添加的噪声都是已知的，逆向过程我们的总体目标就是希望通过网络预测这些添加的噪声然后一步步去噪声。和前向过程类似，逆向过程我们也写成两种形式：
单步逆向:中间某个逆向过程(从
)可表示为条件概率: 总体逆向:整个逆向过程的(从
)可以表达为联合概率:
【其实上面的
其实如果我们知道其真实的逆过程
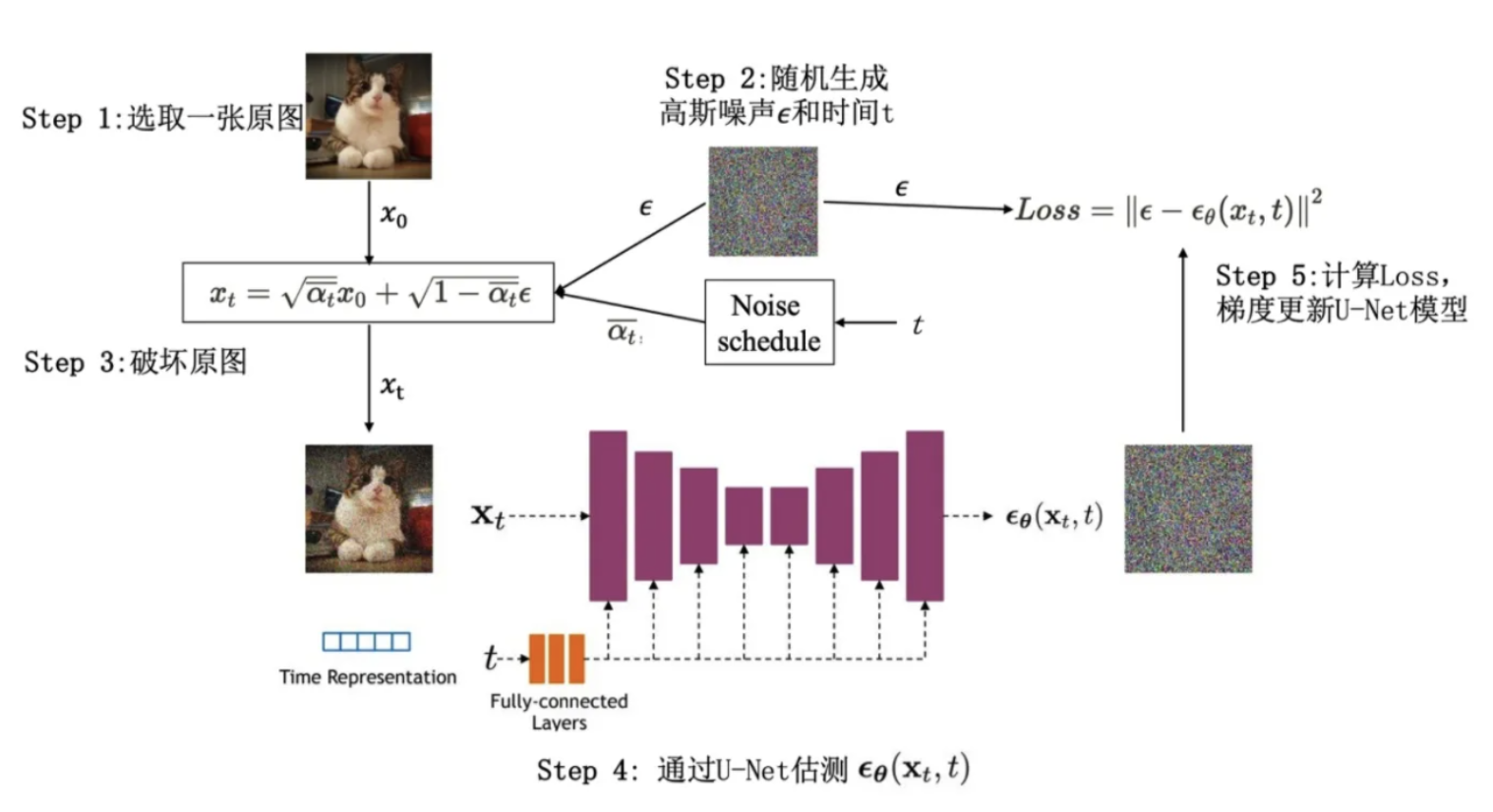
训练过程
损失函数形式
根据逆向过程中的阐述，Diffusion训练的主要目标就是计算用于预测噪声均值和方差的网络
题外话:这里还可以利用KL散度的非负性配合Fubini定理也可以得到类似的结果:
这里再进一步对
【上面最后一步推理其实还是没有特别搞懂，期望
整理上面的公式可以得到我们要优化的损失函数
损失函数拆解-L_0和L_T
损失函数中的
损失函数拆解-L_{t-1}
重点讨论损函数中的
这时候我们发现上面
通过上面我们其实可以看到方差
上面推了这么多公式，可能会有点忘记最初的目标，到此我们回过头再捋一下思路：Diffsion训练的主要目标就是计算用于预测噪声均值和方差的网络
【其实换个角度来说，
计算高斯分布对的KL散度
在计算公式(15)中的高斯分布pair对的KL散度前，DDPM论文中
根据上面固定方差的前提，那么我们就可以进一步简化公式(15):
【其中第三行用到了对角矩阵的逆等于该对角矩阵对角线上每个元素取倒数】
由公式(17)我们其实可以发现了！！在固定方差
到这里再捋一次思路:通过上面一系列式子的推导可以看到我们需要优化的总体损失函数
从上面其实就可以看到我们在固定方差预测
此外我们回头看一下公式(5)，其中的均值预测网络
总结
根据公式(14)总结一下Diffusion的训练过程：
- 随机选择一个训练样本
，从 的前向过程随机选择一个时间戳t，从高斯噪声 中采样随机噪声 - 计算第
步加噪的结果 - 将
和时间戳t送入到噪声预测网络得到预测噪声 - 根据预测的噪声
和真实噪声 计算L2/L1损失并进行梯度下降
网络
- 从高斯噪声
中采样随机噪声 - 根据公式(21)可以进行逆向过程从
预测得到得到去噪后的 - t从T到1不断重复上面过程，直至最后完成新样本的生成
训练过程示意图可以表示为下面这样:
思考和QA环节
以下思考和回答都是我在推导DDPM公式的时候突然想到的，回答也是基于自己的理解进行解释，如有问题，欢迎指出~
Q: 公式(1)中均值系数直接设置为
，为什么要和方差系数扯上关系？：
A: 通过公式(3)或者公式(4)可以看到在设定了均值系数为且 在0~1范围后，当前向过程足够久的时候，即 时，均值 ，方差 ，这时候就保证 的分布收敛于一个标准的高斯分布 。同时我也推理了一下如果就是普通的均值 ,那么在T=3时候有: 可以看到均值系数 是连乘的形式，这只需要每一项 就能保证连乘的结果趋近于0即均值系数为0了，对于方差部分在均值系数设置为 是一个可以保证 时方差收敛于1的解，至于还有没有其他解法:cry:本人暂时有限，也欢迎大家评论补充。 Q：公式(20)直接将每个KL散度的系数去掉了，会不会有什么副作用？
A：由于去掉了不同的权重系数，所以这个简化的目标其实是对原本损失中进行了reweight。对于这种reweight，先将系数 随着时间 的变化函数画出来如下:其中 按照DDPM论文中取在 范围均匀采样1000次(如下图所示),从下图可以看到虽然不是严格单调递减，但是总体趋势是：随着t的增加， 的权重系数越来越小，所以DDPM论文中的说法是:reweight相比较而言降低了在 较小时候的损失权重而增加了 在较大时候的损失权重(因为全部都变成了1)，而在 较小的时候(即已经接近原图 时)，这时候去噪使用的噪声已经很少了，所以降低他们的权重对于整体的网络训练是有好处的，而在 较大的时候(即降噪初期)，降噪任务相对较难，reweight也能够使网络更加专注于t较大时候的去噪。 
Q：根据公式 (3)知道
是从 直接计算 使用的噪声，而 根据公式(5)知道其是在从 预测 使用的噪声，虽然都是服从标准高斯分布，但是从数值上看应该是两个不同的噪声吧？两个能直接计算L2损失?
A：表扬下自己，感觉思考还是比较深入。我的理解如下:也确实是从 直接计算 使用的噪声，但是回顾一下 的定义，其就是为了单纯拟合 的并没有什么有实际含义的物理定义，如果非要有什么明确的物理含义，那么可以认为 的目的就是去预测从 计算 所使用的噪声。 Q：既然
就是去预测从 计算 所使用的噪声，那么这里为什么这里能够直接在 到 的时候使用这个噪声进行去噪？
A：我想的是这里只是用到了这个变量，而不仅仅就是简单地用 减去 去噪得到了 ，其实仔细想想， 是为了计算 到 用到的噪声的均值-即公式(14-3)的 ，通过这个这个噪声均值和方差 再去得到 的，至于为什么能通过预测的 的噪声 来计算 的噪声均值，那就是公式(18)做的事情。 Q：有一个可能比较蠢但是对于理解含隐变量生成模型比较有帮助，就是如果我们的损失函数是为了保证网络预测的噪声/均值和原本前向过程使用的噪声/均值完全一致，而前向的噪声是我们自己指定的，肯定是已知的，那么在反向生成的过程中直接就用原始前向过程中实际用到的噪声不就能去噪了吗？
A：首先肯定的是：直接用前向的噪声去噪，肯定是能恢复得到原始输入图像的(其实就是加一减一等于自己的过程)，但是问题就在这里了，这时候我们也就只能去噪得到训练集中的原始输入图像了，无法生成其他图像，因为我们想生成其他不存在的图像，但是现在我们拿到手的只有最原始的噪声啊，我们不知道他在前向过程中是怎么加噪得到的，所以我们这才需要通过额外训练好的网络来"想象"它被添加了哪些噪声，然后进行去噪。其实想一下VAE的过程就知道了，VAE的目标其实就是重构原图，其将一个原图映射到一个高斯分布的隐空间，然后再从隐空间回到图像空间，看起来也是一个加一减一的相反过程，但是其能保证在训练完成后我们在隐空间随便采样(尤其是对于其原来没见过的样本)时，都能够用原本VAE的能力生成对应的图像。所以相当于来说VAE是学到了从隐空间映射到图像空间的能力，而Diffusion是学到了从采样噪声中预测噪声的能力来去噪生成图像(采样噪声-预测噪声=生成图像)，两者的相似性在于VAE中的encoder对应Diffusion的前向过程，VAE中的decoder对应Diffusion中的逆向过程。
✅2023.8.25补充:
Q：DDPM代表的Diffusion模型为什么要迭代优化，不能一次性添加噪声一次性预测噪声吗？
DDPM的加噪和去噪都是一个马尔科夫链的过程，加噪是在上一步的结果上继续添加噪声，并且在上述公式(4)也表明了只有在添加噪声次数足够多(T足够大)的情况下，最终的加噪结果才是符合高斯分布的。那么问题又来到“我们为什么要将噪声变成纯高斯噪声？我们一次性在原图上加大幅度的噪声不就让原图变得噪乱不堪了吗？”这没错，但是你知道这时候的噪声图像是什么分布吗？如果不知道的话，我们怎样在训练完模型后采样这个原始噪声进行去噪生成呢？没办法了啊！所以为了好采样，我们要求噪声符合高斯分布，而让一张原始图变成高斯分布，又需要通过马尔科夫链的形式将其一步步变成纯高斯噪声。
其实一步步添加小噪声的另一个好处是降低逆向过程中噪声预测的难度，提升生成效果！