问题概述
众所周知，神经网络权重不能初始化为常数，更不能全部初始化为0。依据反向传播的思想可知：每个权重的更新梯度与其之后相关的权重、神经元的输入、输出和其前一个神经元的输出有关(这里不进行具体推导)。网上很多相关文章说不能初始化为0或者常数，这个结论肯定是正确的。但是原因却不是这样会导致权重不更新了。其实完全错误，只要有误差，就会更新。
神经网络模型定义
现假设神经网络的通用形式如下：
有一个输入层，n个隐藏层，一个输出层。其中输入层和第1个隐藏层的参数权重为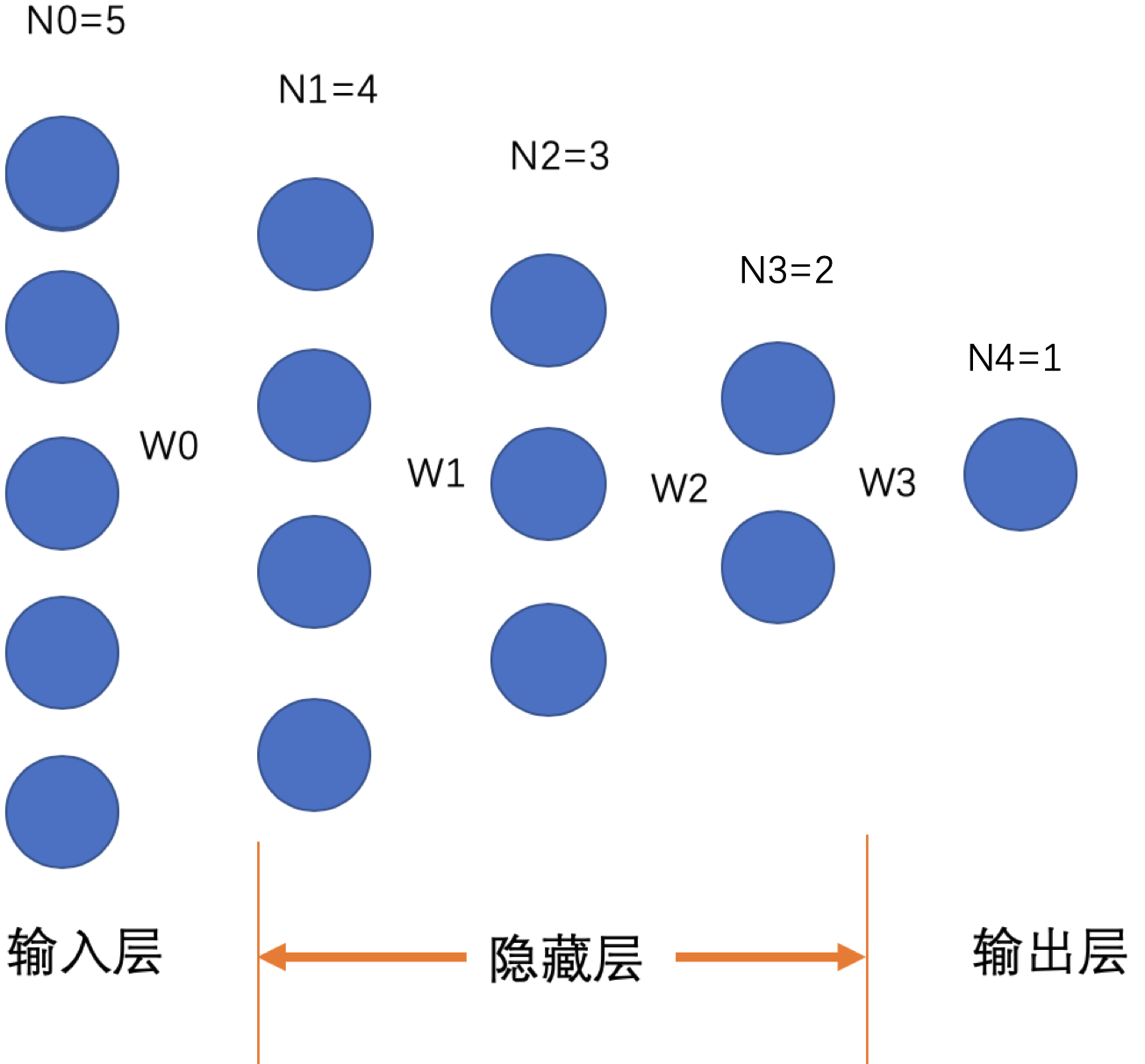
思考推导
现在有两种权重初始化的方式:
1.若全初始化为0。则第k次反向传播后，倒数第
2.若全部初始化为非0。则每次反向传播后，每个权重内部的元素都相等且不为0(除
中来自同一个输入神经元的权重是相等的，即对每一个固定 ， 都是相等的，其中 ，即 每行是相等的。 除
外每个权重各自内部的元素都均是相等的，且相同隐藏层的神经元输入是相等的、输出也是相等。这就会导致每个隐藏层都退化成实际上只有1个神经元。(也就是说整个神经网络处于对称状态，被线性化了，注意不是变成了线性网络，因为还有非线性的激活函数存在)。
那么为了打破这种对称状态，现在如果仅仅将第一权重
3.若对
4.若对
如果推广到更一般的情况：即将前M个权重随机初始化，后面的权重依然分为初始化为0和非0
常数，即： 1和3的一般形式: 前M个权重是随机初始化，
2和4的一般形式： 前M个权重是随机初始化，
到 是仍然"随机"， 是行相等的， 之后每个权重是内部相等的且第 个及之后的隐藏层内每个神经元的输入时相等的、输出是相等的、权重是完全相等的。
最终结论!!!!
如果前M个权重是随机初始化，其余权重全部初始化为同一个值(或者每一个权重内部各自初始化为相等的元素)，则最后陷入的状态是:
到 是仍然"随机"， 是行相等的， 之后每个权重是内部相等的且第 个及之后的隐藏层内每个神经元的输入时相等的、输出是相等的、权重是完全相等的。
以上其实就是将原本输入层向后推到了第M个隐藏层作为真实输入层，所以更一般的表述为：真实输入层之后的那个权重最终状态是行相等的，再之后的每个权重的内部元素是各自相等的，真实输入层之前的权重仍然是"随机"的。 而是否初始化为0 ,只是过程有区别：其中如果真实输入层之后全部初始化为0，那么在过程中会随着反向传播从最后一个权重逐步向前依次将之前的权重变成非0值；而如果真实输入层之后每个权重内部各自初始化为相等的值，那么其在第一次反向传播后，就已经达到了最终状态。
其实这样也证明了为什么逻辑斯特线性回归可以将权重全部初始化为0，因为其没有隐藏层，其唯一的权重是
实验证明
import tensorflow as tf
import numpy as np
#随机初始化的权重
random_inds = [-1]
class NeuralNetWork:
def __init__(self, node_nums, weight_init, bias_init):
if not isinstance(weight_init, type([])):
weight_init = [weight_init] * (len(node_nums) - 1)
if not isinstance(bias_init, type([])):
bias_init = [bias_init] * (len(node_nums) - 1)
print("Nodes:{},weight_init:{},bias_init:{}".format(node_nums, weight_init, bias_init))
self.layers = len(node_nums)
self.weight = []
self.bias = []
for ind, num in enumerate(node_nums[:-1]):
self.weight.append(tf.Variable(
tf.constant(value=weight_init[ind], dtype=tf.float32, shape=[node_nums[ind], node_nums[ind + 1]])))
self.bias.append(tf.Variable(
tf.constant(value=bias_init[ind], dtype=tf.float32, shape=[node_nums[ind + 1], 1])))
#将偏置随机初始化可以打破对称
# self.bias.append(
# tf.random_normal(shape=[node_nums[ind + 1], 1], mean=0.0, stddev=1.0, ))
#随机化指定的权重
for random_ind in random_inds:
if (random_ind >= 0):
self.weight[random_ind] = tf.random_normal(shape=[node_nums[random_ind], node_nums[random_ind + 1]],
mean=0.0, stddev=1.0, )
def forward(self, x):
node_out = [x]
net = x
for ind in range(self.layers - 1):
net = tf.matmul(tf.transpose(self.weight[ind]), net) + self.bias[ind]
net = tf.sigmoid(net) # 如果不加激活函数,那么在权重全部初始化为0时,权重就真的不会更新,永远为0
node_out.append(net)
return net, node_out
def mse_loss(self, pred, gt):
return tf.reduce_mean((pred - gt) ** 2)
def train():
input_dim = 5
out_dim = 2
x_placeholder = tf.placeholder(tf.float32, [input_dim, 1])
gt_placeholder = tf.placeholder(tf.float32, [out_dim, ])
net = NeuralNetWork([input_dim, 4, 3, 2, out_dim], 0.0, [0.1, 0.2, 0.3, 0.4])
pred, nodes_out = net.forward(x_placeholder)
mse_loss = net.mse_loss(pred, gt_placeholder)
train_op = tf.train.GradientDescentOptimizer(0.8).minimize(mse_loss)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for _ in range(6):
x = np.random.randn(input_dim, 1)
y = np.ones(shape=[out_dim, ])
# 查看每个隐藏层的输出
# nodes_out_ = sess.run(nodes_out, feed_dict={x_placeholder: x, gt_placeholder: y})
# for node_out in nodes_out_:
# print(node_out)
sess.run(train_op, feed_dict={x_placeholder: x, gt_placeholder: y})
weights, bias = sess.run([net.weight, net.bias])
print("step:{}".format(_))
# 查看权重变化
for weight in weights:
print(weight)
# 查看权重变化
for bias_ in bias:
print(bias_)
print("------------------")
if __name__ == '__main__':
train()如上，我将权重全部初始化为0，且输出层有两个神经元(这不影响结果)，每次权重更新后的结果如下:
可以看到，随着每次迭代和反向传播，会从最后一个权重向前，逐渐将权重打破0值，但是仍然实现相等的，在一开始的网络结构下(最上面的网络图)，有4层权重，所以在第四次迭代后，就已经进入平衡状态了。
其实有个简单的打破平衡状态的方法，就是即便权重初始化为0，但是偏置是随机初始化。因为这样就能保证每个隐藏层内的神经元输出是不同的了。有兴趣的同学可以自行尝试。
思考：
1.如果只将某个权重随机化，那么反向传播后其前面一个权重是列相等的。如随机初始化
请有想法的人随时交流~